Glossary
Ένα χρήσιμο γλωσσάριο για να μην ξεχνάμε βασικούς ορισμούς!
Special | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | ALL
Δ |
|---|
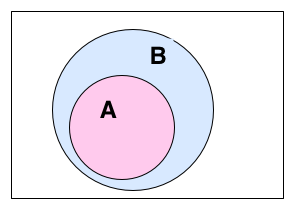
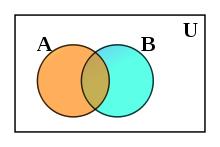
Διαγράμματα VennΔιάγραμμα Venn είναι μια απεικόνιση συνόλων. Σε κάθε διάγραμμα Venn υπάρχουν:
Στο διάγραμμα Venn η κάθε επιφάνεια που ορίζεται από οποιοδήποτε συνδυασμό γραμμών συμβολίζει ένα σύνολο. Έτσι είναι λάθος να υπάρχει επιφάνεια που δεν αντιστοιχεί σε κάποιο σύνολο. Μερικές φορές σε ένα διάγραμμα Venn συμβολίζονται μερικά στοιχεία συνόλων με κουκίδες, τα οποία μπορεί να συνοδεύονται από το αντίστοιχο σύμβολο του στοιχείου που απεικονίζουν. Όλα τα στοιχεία ενός διαγράμματος Venn βρίσκονται μέσα στο ορθογώνιο.
|
Μ |
|---|
ΜεταβλητήΗ έννοια της μεταβλητής είναι αρχική έννοια για τα Μαθηματικά, δηλαδή τη δεχόμαστε αξιωματικά, χωρίς απόδειξη. Μια μεταβλητή είναι ένα γράμμα που μπορεί να περιέχει που συμβολίζει ένα τυχαίο στοιχείο ενός συνόλου και χρησιμεύει για να δηλωθεί μια κοινή ιδιότητα των στοιχείων του. Μια μεταβλητή «διατρέχει» όλα τα στοιχεία του συνόλου στο οποίο αναφερόμαστε (σύνολο αναφοράς). Επίσης όταν χρειάζεται χρησιμοποιούνται κεφαλαία γράμματα και δείκτες. Συνήθως ως μεταβλητές χρησιμοποιούνται τα τελευταία μικρά γράμματα της ελληνικής ή της αγγλικής αλφαβήτου. Μια ιδιότητα που εκφράζεται για ορισμένα στοιχεία ισχύει μόνο για αυτά, ενώ όταν δηλώνεται μια ιδιότητα για μια μεταβλητή, ισχύει για όλα τα στοιχεία του συνόλου. |
Π |
|---|
Πεδίο ΟρισμούΠεδίο Ορισμού ονομάζεται το υποσύνολο Α του R, από το οποίο παίρνει τιμές η μεταβλητή x ( η οποία ονομάζεται και ανεξάρτητη μεταβλητή). Το Πεδίο Ορισμού (Π.Ο) είναι το σύνολο Α στα διαγράμματα του Venn, απ' όπου "ξεκινούν τα βέλη" ή το σύνολο που "τροφοδοτεί" την "μηχανή" της συνάρτησης |
Πεδίο ΤιμώνΠεδίο Τιμών Ονομάζεται το υποσύνολο Β του R, απο το οποίο παίρνει τιμές η μεταβλητή y ( η οποία ονομάζεται εξηρτημένη μεταβλητή). Το πεδίο τιμών Β είναι το σύνολο που "καταλήγουν τα βέλη", στα διαγράμματα του Venn, ή το "κουτί που βγαίνουν" οι τιμές από τη "μηχανή" της συνάρτησης.
|
Σ |
|---|
ΣυνάρτησηΣυνάρτηση είναι μια αντιστοίχιση μεταξύ δύο συνόλων A και Β, που καλούνται σύνολο ορισμού και σύνολο τιμών αντίστοιχα, κατά την οποία κάθε ένα στοιχείο x του συνόλου ορισμού Α αντιστοιχίζεται σε ένα και μόνο στοιχείο y του συνόλου τιμών Β. Αν Α και Β είναι τα δύο σύνολα, γράφουμε f : Α → Β. Τα σύνολα Α και Β είναι συνήθως υποσύνολα του συνόλου των Πραγματικών Αριθμών R. |
Σύνολα ΑριθμώνΤα σύνολα των αριθμών είναι ..... τα εξής: |
ΣύνολοΣύνολο ονομάζουμε κάθε συλλογή M, (σαφώς) διακριτών αντικειμένων m (που ονομάζουμε «στοιχεία» του συνόλου M), της διαίσθησης ή της σκέψης μας, που θεωρούμε ως ολότητα. Τα αντικείμενα αυτά καλούνται στοιχεία του συνόλου και μπορούν να είναι οτιδήποτε, από αριθμούς μέχρι ανθρώπους ή γράμματα του αλφαβήτου. Ένα σύνολο λοιπόν αποτελείται από στοιχεία. Στοιχεία ενός συνόλου μπορεί να είναι άλλα σύνολα ή και σύνολα συνόλων. Αν το στοιχείο x ανήκει στο σύνολο Α τότε λέμε ότι το στοιχείο x περιέχεται στο σύνολο A ή ότι το σύνολο A περιέχειτο στοιχείο x ή ακόμα ότι το στοιχείο x είναι μέλος του συνόλου A. Χρησιμοποιούμε το συμβολισμό |
Υ |
|---|
ΥποσύνολοΈνα σύνολο X ονομάζεται υποσύνολο ενός συνόλου Y και συμβολίζουμε με Ακόμα χρησιμοποιούμε την ορολογία: το σύνολο X περιέχεται στο σύνολο Y ή ακόμα ότι το σύνολο Y είναι υπερσύνολο του συνόλου X και γράφουμε Παραδείγματα:
Αναφέρουμε ότι: το κενό σύνολο
|
Υποσύνολο ΓνήσιοΑν το σύνολο Χ είναι υποσύνολο του Υ αλλά Χ Για παράδειγμα το σύνολο των φυσικών αριθμών είναι γνήσιο υποσύνολο αυτού των ακεραίων, το σύνολο τον ακεραίων γνήσιο υποσύνολο αυτού των ρητών και το σύνολο των ρητών γνήσιο υποσύνολο των πραγματικών. |
 αν το x ανήκει στο A και το συμβολισμό
αν το x ανήκει στο A και το συμβολισμό  αν το x δεν ανήκει στο A
αν το x δεν ανήκει στο A , εάν κάθε στοιχείο του X είναι και στοιχείο (ανήκει) του Y δηλαδή ισχύει:
, εάν κάθε στοιχείο του X είναι και στοιχείο (ανήκει) του Y δηλαδή ισχύει:
 ως τη
ως τη 

 είναι υποσύνολο κάθε συνόλου και επίσης κάθε σύνολο Α είναι υποσύνολο του εαυτού του.
είναι υποσύνολο κάθε συνόλου και επίσης κάθε σύνολο Α είναι υποσύνολο του εαυτού του. για κάθε σύνολο Α
για κάθε σύνολο Α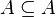 για κάθε σύνολο Α
για κάθε σύνολο Α Υ, δηλαδή αν υπάρχει τουλάχιστον ένα στοιχείο του Υ το οποίο να μην ανήκει στο Χ, τότε λέμε ότι το σύνολο Χ είναι γνήσιο υποσύνολο του Υ και το συμβολίζουμε με
Υ, δηλαδή αν υπάρχει τουλάχιστον ένα στοιχείο του Υ το οποίο να μην ανήκει στο Χ, τότε λέμε ότι το σύνολο Χ είναι γνήσιο υποσύνολο του Υ και το συμβολίζουμε με  ή με
ή με  .
.